Understanding Big-O Notation
Big-O notation describes how the runtime or memory usage of an algorithm grows relative to the size of the input (n).
It focuses on scalability rather than exact speed.
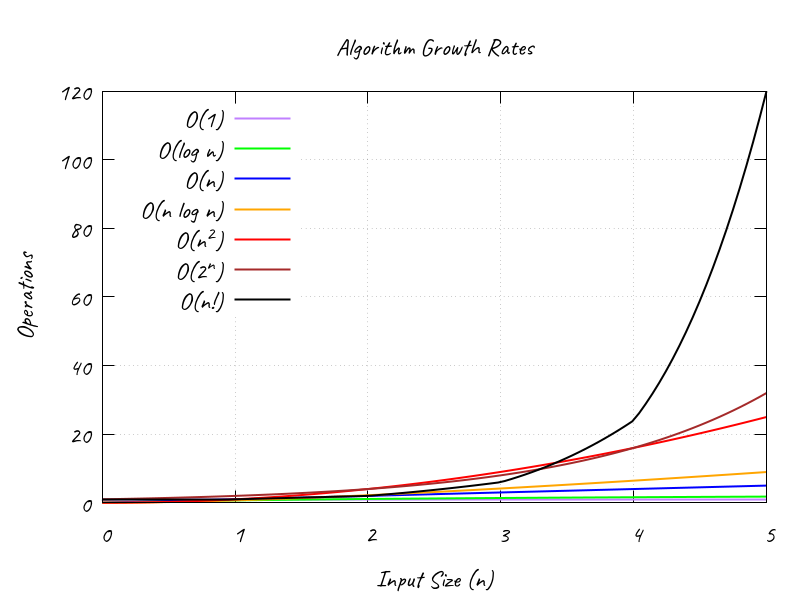
Common Complexities with Examples
O(1) – Constant Time
The runtime does not depend on input size.
def get_first_element(arr):
return arr[0]
O(log n) – Logarithmic Time
Typical in divide-and-conquer strategies (e.g., binary search).
def binary_search(arr, target):
low, high = 0, len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
O(n) – Linear Time
The runtime grows proportionally with input size.
def find_max(arr):
max_val = arr[0]
for x in arr:
if x > max_val:
max_val = x
return max_val
O(n log n) – Linearithmic Time
Efficient sorting algorithms (e.g., mergesort).
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
O(n²) – Quadratic Time
Often comes from nested loops.
def has_duplicates(arr):
for i in range(len(arr)):
for j in range(i + 1, len(arr)):
if arr[i] == arr[j]:
return True
return False
O(2^n) – Exponential Time
Typical of brute-force recursive algorithms.
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)
O(n!) – Factorial Time
Arises in permutation-based solutions (e.g., travelling salesman).
import itertools
def all_permutations(arr):
return list(itertools.permutations(arr))